The Exponentiated Generalized Reduced Kies Distribution with Properties and Applications on Burr Measurement Datasets
DOI:
https://doi.org/10.56532/mjsat.v5i4.542Keywords:
Reduced Kies Distribution, Exponentiated Generalized , Unit-Bounded Distributions, Family of Distributions, Burr Measurement DataAbstract
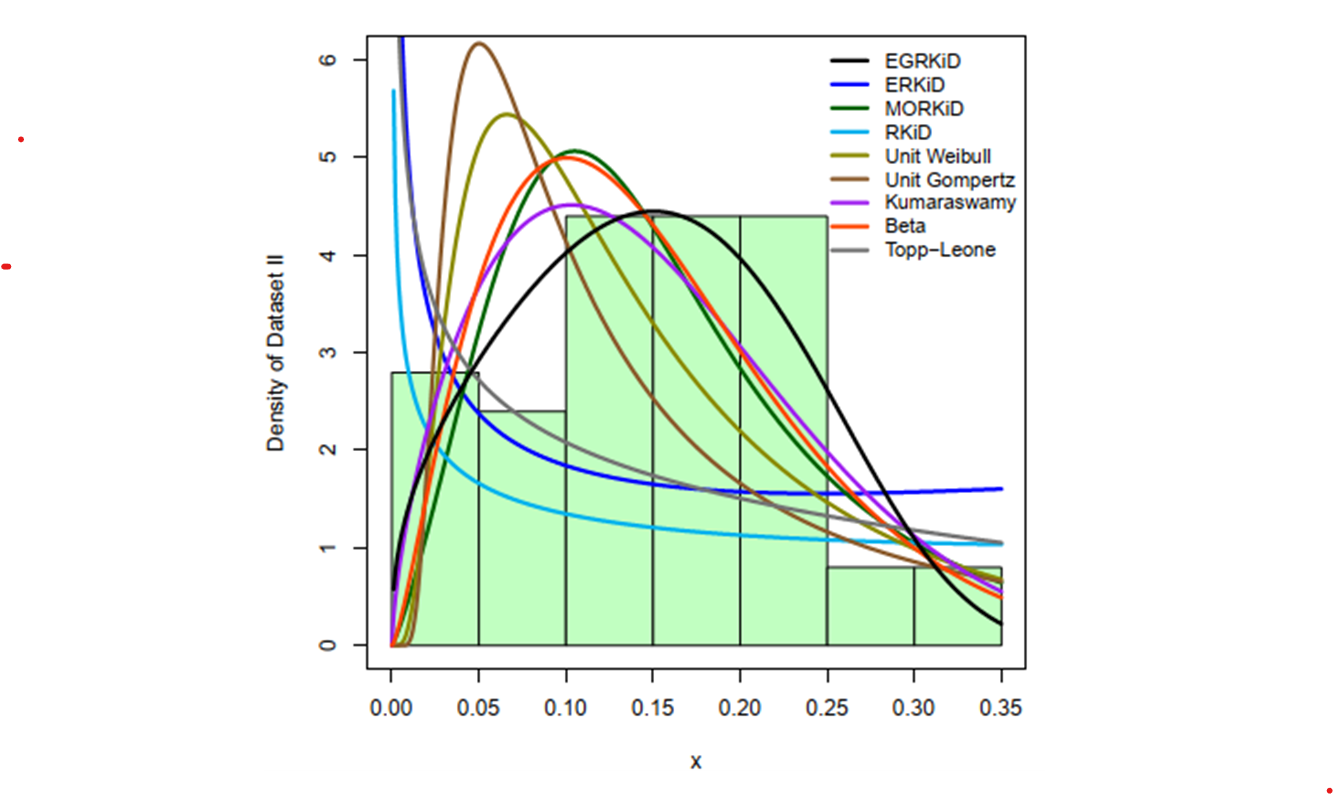
This study introduces and examines a new three-parameter generalized extension of the Reduced Kies distribution, termed the Exponentiated Generalized Reduced Kies Distribution (EGRKiD). Various statistical and mathematical properties of the proposed model are derived, including its quantile function, median, order statistics, skewness, and kurtosis. In addition, key reliability characteristics such as the survival and hazard rate functions are explored. Parameter estimation is performed using maximum likelihood estimation (MLE) and maximum product spacing (MPS), with simulations showing that MLE consistently outperforms MPS, exhibiting up to 40% lower bias and 35% lower mean squared error particularly for samples less than 100. Lastly, the applicability and flexibility of the new distribution are demonstrated through its application to two real burr measurement datasets, where it outperforms eight established unit-bounded distributions. The results show that the EGRKiD provides a superior fit, reducing the AIC by 12-18% and the BIC by 10-15% compared to the next best model. Several goodness-of-fit tests further confirm its advantage, with the EGRKiD yielding KS statistics 50-60% smaller and p-values 3-5 times higher than competing models. These findings highlight the EGRKiD’s flexibility and robustness, making it a valuable tool for applications in engineering and other related fields.
References
G. M. Cordeiro, E. M. Ortega, and D. C. da Cunha, “The Exponentiated Generalized Class of Distributions,” J. Data Sci., vol. 11, no. 1, pp. 1–27, 2013. doi: https://doi.org/10.6339/JDS.2013.11(1).1086
I. Elbatal and H. Z. Muhammed, “Exponentiated Generalized Inverse Weibull Distribution,” Appl. Math. Sci., vol. 8, no. 81, pp. 3997–4012, 2014. doi: https://doi.org/10.12988/ams.2014.44256
P. E. Oguntunde, O. A. Odetunmibi, and A. O. Adejumo, “On the Exponentiated Generalized Weibull Distribution,” Indian J. Sci. Technol., vol. 8, no. 35, pp. 1–7, 2015. doi: https://doi.org/10.17485/ijst/2015/v8i35/85942
H. M. Reyad et al., “The Exponentiated Generalized Topp Leone-G Family of Distributions,” Pak. J. Stat. Oper. Res., vol. 15, no. 1, pp. 1–24, 2019. doi: https://doi.org/10.17485/ijst/2015/v8i35/85942
M. El-Morshedy et al., “Exponentiated Generalized Inverse Flexible Weibull Distribution,” Commun. Math. Stat., vol. 10, no. 3, pp. 413–434, 2021. doi I: https://doi.org/10.1007/s40304-021-00246-7
N. Poonia and S. Azad, “A New Exponentiated Generalized Linear Exponential Distribution,” Res. Math. Stat., vol. 8, no. 1, p. 1953233, 2021. doi: https://doi.org/10.1080/27658449.2021.1953233
E. A. Elsherpienyi and E. M. Almetwally, “The Exponentiated Generalized Power Exponential Distribution,” Pak. J. Stat. Oper. Res., vol. 18, no. 2, pp. 349–367, 2022. doi: https://doi.org/10.18187/pjsor.v18i2.3786
L. B. S. Telee, M. Karki, and V. Kumar, “Exponentiated Generalized Exponential Geometric Distribution,” Interdiscip. J. Manage. Soc. Sci., vol. 3, no. 2, pp. 37–60, 2022. doi: https://doi.org/10.3126/ijmss.v3i2.47862
A. E. EL-Hady et al., “Discrete Exponentiated Generalized Family of Distributions,” Comput. J. Math. Stat. Sci., vol. 2, no. 2, pp. 303–327, 2023. doi: https://doi.org/10.21608/cjmss.2023.203704.1014
K. Keganne et al., “A New Extension of the Exponentiated Generalized-G Family,” Sci. Afr., vol. 20, p. e01719, 2023. doi: https://doi.org/10.1016/j.sciaf.2023.e01719
A. I. L. Abonongo and J. Abonongo, “Exponentiated Generalized Weibull Exponential Distribution,” Comput. J. Math. Stat. Sci., vol. 3, no. 1, pp. 57–84, 2024. doi: https://doi.org/10.21608/cjmss.2024.275771.1059
M. Kpangay, “On the Exponentiated Generalized Exponentiated Exponential Distribution,” Int. J. Sci. Res. Eng. Dev., vol. 6, no. 1, pp. 941–951, 2023.
Y. Altinisik and E. Çankaya, “Exponentiated Generalized Ramos-Louzada Distribution,” Commun. Fac. Sci. Univ. Ankara Ser. A1 Math. Stat., vol. 73, no. 1, pp. 76–103, 2024. doi: https://doi.org/10.31801/cfsuasmas.1285065
I. Sule et al., “A New Generalized Exponentiated Family,” Reliab. Theory Appl., vol. 20, no. 1 (82), pp. 38–52, 2025.
C. S. Kumar and S. H. S. Dharmaja, “On Reduced Kies Distribution,” Collect. Recent Stat. Methods Appl., pp. 111–123, 2013.
F. G. Akgül, “Comparison of Estimation Methods for Exponentiated Reduced Kies Distribution,” Süleyman Demirel Univ. Fen Bilim. Enstitüsü Derg., vol. 22, no. 3, pp. 1209–1216, 2018. doi: https://doi.org/10.19113/sdufbed.08036
I. Usta and M. Akdede, “Bayesian Estimation of the Reduced Kies Distribution Parameters,” Proc. Book, p. 138, 2019.
C. S. Kumar and S. H. S. Dharmaja, “The Exponentiated Reduced Kies Distribution,” Commun. Stat. Theory Methods, vol. 46, no. 17, pp. 8778–8790, 2017. doi: https://doi.org/10.1080/03610926.2016.1183786
A. A. Al-Babtain et al., “A New Modified Kies Family,” Math., vol. 8, no. 8, p. 1345, 2020. doi: https://doi.org/10.3390/math8081345
M. A. Almuqrin et al., “A Flexible Extension of Reduced Kies Distribution,” Complexity, vol. 2022, Article ID 6078567, 2022. doi: https://doi.org/10.1155/2022/6078567
A. L. Bowley, Elements of Statistics, 6th ed. London: Staples Press, 1937.
J. J. A. Moors, “A Quantile Alternative for Kurtosis,” J. Roy. Stat. Soc. Ser. D (Statistician), vol. 37, no. 1, pp. 25–32, 1998. doi: https://doi.org/10.2307/2348376
A. Z. Afify et al., “A New Unit Distribution,” Electron. J. Appl. Stat. Anal., vol. 15, no. 2, pp. 460–484, 2022. doi: https://doi.org/10.1285/i20705948v15n2p460
S. Nadarajah and S. Kotz, “Moments of Some J-Shaped Distributions,” J. Appl. Stat., vol. 30, pp. 311–317, 2003. doi: https://doi.org/10.1080/0266476022000030272
F. Sultana et al., “Parameter Estimation for the Kumaraswamy Distribution,” Am. J. Math. Manage. Sci., vol. 37, no. 3, pp. 243–261, 2018. doi: https://doi.org/10.1080/01966324.2018.1458166
N. L. Johnson, S. Kotz, and N. Balakrishnan, Continuous Univariate Distributions, 2nd ed., vol. 2. Wiley, 1994.
J. Mazucheli, A. F. B. Menezes, and M. E. Ghitany, “The Unit-Weibull Distribution,” J. Appl. Probab. Stat., vol. 13, no. 2, pp. 1–22, 2018. doi: https://doi.org/10.1155/2018/2303796
J. Mazucheli, A. F. B. Menezes, and S. Dey, “Unit-Gompertz Distribution,” Statistica, vol. 79, no. 1, pp. 25–43, 2019 doi: https://doi.org/10.6092/issn.1973-2201/8497
P. R. D. Marinho et al., “AdequacyModel: An R Package,” PLoS One, vol. 14, no. 8, p. e0221487, 2019. doi: https://doi.org/10.1371/journal.pone.0221487
R. Dasgupta, “On the Distribution of Burr,” Sankhya B, vol. 73, pp. 1–19, 2011. doi: https://10.1007/s13571-011-0025-9
R. A. ZeinEldin et al., “Different Estimation Methods for Type I Half-Logistic Topp–Leone Distribution,” Math., vol. 7, no. 10, p. 985, 2019. doi: https://10.3390/math7100985
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2025 Ehinomen Emmanuel Ehizojie

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.


